UJI SATU POPULASI
UJI SATU POPULASI
Pengantar
Uji statistik untuk satu populasi dimaksudkan untuk melakukan pengujian hipotesis pada satu populasi. Pengujian hipotesis ini biasa sering disebut pengujian hipotesis deskriptif.
Statistik parametrik yang dapat digunakan untuk menguji hipotesis diskriftif bila datanya berbentuk interval atau rasio adalah uji t-test 1 sampel.
http://bahankuliahkesehatan.blogspot.com
Rumus
Rumus yang biasa digunakan adalah
Contoh kasus
Suatu penelitian dilakukan di UGM terhadap 10 mahasiswa terhadap berat badan mahasiswa. Seorang peneliti menduga bahwa berat badan mahasiswa UGM = 65 kg.
Ujilah hipotesis peneliti tersebut dengan uji beda mean.
Berdasarkan hasil penelitian diperoleh hasil sebagai berikut:
| No | BB MHS |
| 1 | 68 |
| 2 | 63 |
| 3 | 46 |
| 4 | 62 |
| 5 | 64 |
| 6 | 47 |
| 7 | 59 |
| 8 | 44 |
| 9 | 50 |
| 10 | 67 |
Penyelesaian
1. Menentukan Hipotesis
Ho; Berat badan mahasiswa UGM adalah 60 Kg
Ha: Berat badan mahasiswa UGM tidak sama dengan 60 kg
2. Menentukan daerah penerimaan hipotesis
Alfa = 0,05
3. Perhitungan
4. Hasil
5. Kesimpulan
6. Arti
UJI STATISTIK 2 POPULASI
UJI CHI SQUARE
1. Pengantar
Dalam kerangka pengunaan uji chi square, terdapat beberapa uji chi square diantarannya uji chisquare untuk goognes of fit dan uji chi square untuk independensi. Uji statistik chi square dapat digunakan untuk menguji hipotesis bila data populasi terdiri dari 2 atau lebih kelas dan data berbentuk nominal.
Sampel independensi biasanya digunakan dalam penelitian yang mengunakan pendekatan survey, sedangkan sampel yang berpasangan sering di gunakan dalam penelitian eksperimen.
2. Chi square (uji independensi)
Untuk menlakukan analisis chi square kita memerlukan tabel bantu untuk mempermudah perhitungan dengan mengunakan uji chi square. Tabel yang biasa seperti pada format berikut:
Sebuah contoh ilustrasi:
|
Variabel | Variable dependent (kejadian infeksi) | RP/OR/RR | X2 | P | CI 95% | |
| Ya | Tidak | |||||
| Variable independent (kepatuhan bidan) | ||||||
| Ya | A | B | ||||
| Tidak | C | D |
Rumus
Keterangan
Sel A adalah faktor yang terpapar (tidak patuh ) dan terjadi infeksi.
Sel B adalah faktor yang terpapar dan tidak terjadi infeksi
Sel C adalah faktor yang tidak terpapar dan kejadian infeksi
Sel D adalah faktor yang tidak terpapar dan tidak terjadi infeksi.
Suatu contoh
Seorang manajer rumah sakit ingin mengetahui apakah terdapat perbedaan antara laki-laki dan perempuan dalam kedisiplinan bekerja. Kedisiplinan bekerja dalam kasus ini diukur dengan kelengkapan absensi kehadiran kerja setiap hari selama 1 bulan. Jika asumsi kedisiplinan kerja dihitung dengan jumlah tidak pernah absen dalam satu bulan dimana dalam satu bulan terdapat 26 hari kerja efektif. Berdasarkan hasil pengamatan diperoleh data sebagai berikut:
| ID | Jenis kelamin | Kedisiplinan | ID | Jenis kelamin | Kedisiplinan |
| 1 | Laki-laki | 24 | 16 | Perempuan | 23 |
| 2 | Laki-laki | 25 | 17 | Perempuan | 24 |
| 3 | Laki-laki | 25 | 18 | Perempuan | 23 |
| 4 | Laki-laki | 26 | 19 | Perempuan | 23 |
| 5 | Laki-laki | 26 | 20 | Perempuan | 23 |
| 6 | Laki-laki | 26 | 21 | Perempuan | 23 |
| 7 | Laki-laki | 26 | 22 | Perempuan | 26 |
| 8 | Perempuan | 24 | 23 | Perempuan | 26 |
| 9 | Perempuan | 22 | 24 | Laki-laki | 25 |
| 10 | Perempuan | 23 | 25 | Laki-laki | 25 |
| 11 | Perempuan | 24 | 26 | Laki-laki | 26 |
| 12 | Perempuan | 23 | 27 | Laki-laki | 26 |
| 13 | Perempuan | 23 | 28 | Laki-laki | 26 |
| 14 | Perempuan | 23 | 29 | Laki-laki | 26 |
| 15 | Perempuan | 23 | 30 | Laki-laki | 26 |
Dari tabel tersebut diatas kita coba mengunakan tabel bantu sebagai berikut
|
Variabel | Kedisiplinan | RP/OR/RR | X2 | P | CI 95% | |
| Ya | Tidak | |||||
| Jenis kelamin | ||||||
| Laki-laki | 9 | 5 | 12.6 | 6.54 | 0.011 | 1.58-128.38 |
| Perempuan | 2 | 14 |
Kemudian masukkan nilai tersebut kedalam rumus yang ada:
X2=


 05.53
05.53
 Rafless bencoolen
Rafless bencoolen

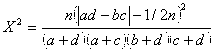

![clip_image006[1] clip_image006[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEg9V8fxGif5qpG8dGtAwt9m-HunUXNjiX8k50qkbrVMI2Cpxr-LY1drHbAjLpi6yl35kmgVch6kVFbfM-nRW0sFMdxSpYAFnyngpwIQm6E7IibiDut5m6oHW-bIkctiwOUSohQGCuykD8s/?imgmax=800)



0 komentar:
Posting Komentar